note_221118

发表于 更新于 分类于
notes for CV while coding

221118

class类中的self属性：

在类(class)的代码中，需要访问当前实例中的变量和函数，可以为类的实例绑定属性的定义.

class中的self：把class中定义的变量和函数定义成实例变量和实例函数

1
2
3
4
5
6
7
8
class Person(object):
    def __init__(self,name,score):
        self.name=name
        self.score=score
      
student=Person('Gavin',100) #创建一个Person类的实例，需要传入__init__方法中需要的参数
print(student.name)  #Gavin
print(student.score) #100

__init__方法的第一个参数永远是self，表示创建的实例本身，因此，在__init__方法的内部就可以把各种属性绑定到self上，而self就指向创建的实例本身。

使用__init__方法后，创建实例就不能再传入空参数，必须传入与__init__方法相匹配的参数，但是不需要传入self。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#在类中定义函数时，第一个传入的参数永远是self，并且在调用时不需传递该参数。但在类内相互调用时，要加self
class Person(object):
    def __init__(self,x,y):
        self.x=x
        self.y=y
      
    def add(self,z): #调用时传入变量z，该变量是普通的局部变量，而非实例变量，若传入实例变量需要在__init__方法中定义self.z=z
        sum=self.x+self.y+z
        return sum
      
    def square(self):
        squr=pow(self.x,2)+pow(self.y,2)
        return squr
  
    def add_squr(self):
        c=self.add(z)+self.square() #调用类内的函数要用self索引
      
student=Person(3,4)
print(student.add(16)) #23
print(student.square()) #25
print(student.add_squr()) #48

私有变量(private)，只有内部可以访问，外部不能访问，私有变量的定义是在名称前以两个下划线开头，例如: __name。

221119

绘制二维高斯分布的拟合图像

%matplotlib inline :内嵌画图，即将所绘制的画布都显示在notebook中

1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
import matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D #绘制3D图的库
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#生成X,Y,Z三个维度的数据
X = np.arange(-3, 3, 1)
#[-3,-2,-1,0,1,2]
Y = np.arange(-2, 2, 1)
#[-2,-1,0,1]
X, Y = np.meshgrid(X, Y) #网格化x,y,统一了x和y的维度
'''
X:4*6
[[-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]]
Y:4*6
[[-2. -2. -2. -2. -2. -2.]
 [-1. -1. -1. -1. -1. -1.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 1.  1.  1.  1.  1.  1.]]
'''
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
1
2
3
4
5
6
fig=plt.figure() #新建一个画布
ax=Axes3D(fig) #将画布3D化
#画图用plot_surface方法
surf=ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()

plot_surface方法的参数

参数 描述
X,Y,Z 2D数组形式的数据值
rstride 数组行距（步长大小）
cstride 数组列距（步长大小）
color 曲面块颜色
cmap 曲面块颜色映射
facecolors 单独曲面块表面颜色
norm 将值映射为颜色的 Nonnalize实例
vmin 映射的最小值
vmax 映射的最大值

$$
Q(y_i=1|x_i)=p(y_i=1|x_i;\theta)=\frac{p(y_i=1,x_i;\theta)}{p(x_i;\theta)}=\frac{p(x_i|y_i=1;\theta)*p(yi=1;\theta)}{p(x_i|y_i=1;\theta)*p(yi=1;\theta)+p(x_i|y_i=0;\theta)*p(yi=0;\theta)}
$$

$$
Q(y_i=0|x_i)=p(y_i=0|x_i;\theta)=\frac{p(y_i=0,x_i;\theta)}{p(x_i;\theta)}=\frac{p(x_i|y_i=0;\theta)*p(yi=0;\theta)}{p(x_i|y_i=0;\theta)*p(yi=0;\theta)+p(x_i|y_i=1;\theta)*p(yi=1;\theta)}
$$

np.sum(x,axis=0) #求每一列的和

np.sum(x,axis=1) #求每一行的和

*同样适用于np.mean()方法

221121

感知机模型中，点到超平面的距离运算：

img

221122

计算机视觉04：神经网络

感知机的实现：已知x（输入层）找到y（输出层）->一个最简单的神经网络，只有输入层和输出层。

在输入层和输出层之间加一层隐藏层(hidden layer)，将原来一层的神经网络变成两层的神经网络，并对该两层的神经网络进行正向传播和反向传播的计算。

一层的神经网络，即感知机的实现：由输入数据X和权重矩阵w，偏置项b来计算分类的得分。

$$
\bold{\hat{s_j}}=w^T\bold{x_j}+\bold{b}
$$

目标是找到最优权重矩阵，通过最小化损失函数的方式实现，

$$
Loss=\frac{1}{N}\sum_{i=1}^{N}{L_i}+\lambda R(W)
$$

其中，L_i的计算有两种方法，分别是SVM分类和softmax分类中的损失函数表达方法

$$
SVM: L_i=\sum_{j\neq y_i}{max(0,s_j-s_{y_i}+1)}\
softmax:L_i=-log(\frac{e^{s_{y_i}}}{\sum_{j}{e^{s_j}}})
$$

一层神经网络：

两层神经网络：

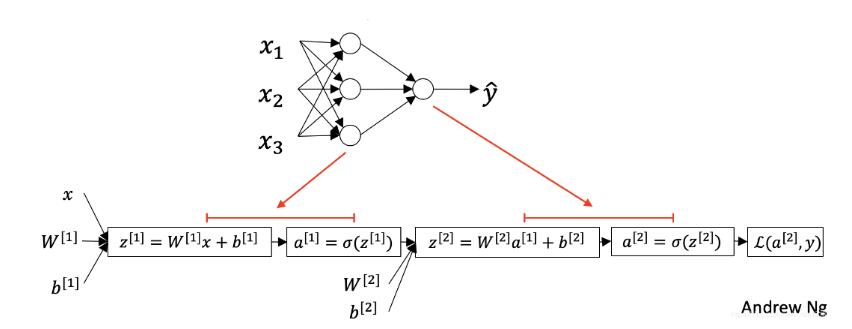
上标[i]表示第i层layer，下标i表示第i个node。

由以上计算过程可以发现，第一层的计算，输入X有三个node，而输出四个node。这四个Node作为下一层的输入，得到3个node分别是x1,x2,x3对应的得分。

通过反向传播，实现梯度下降，得到新的权重矩阵W。

221123

np.prod(a)方法：求数组a或矩阵a中所有元素的乘积，

参数axis=0，按列乘；参数axis=1，按行乘。

np.linspace()方法：创建等差数列

对于数组的reshape方法：x.reshape(x.shape[0],-1)意味着根据x.shape[0]的参数计算出另一个维度的参数。

np.maximum(x,y)方法：逐个元素比较，对应每个位置，在x,ylist中取大。

random.randint(low,high=None,size=None,dtype=’1’)：随机生成size个[low,high)之间的数，若没有high，则生成size个在[0,low)之间的数。

np.random.normal（loc,std,shape）:生成符合高斯分布的数 params:(均值，方差，形状)

python assert（断言）：用于判断一个表达式，在表达式条件为 false 的时候触发异常。

y=np.asarray([0,5,1])：y=[0,5,1] (array)

221124

梯度爆炸

什么是梯度爆炸？

梯度爆炸是指神经网络在训练过程中大的误差梯度不断积累，导致模型权重出现重大更新，造成模型不稳定，无法利用训练数据学习。
误差梯度是神经网络训练过程中计算的方向和数量，用于以正确的方向和合适的量更新网络权重。在深层网络中，误差梯度可在更新中积累，变成非常大的梯度，这样会导致网络权重的大幅更新，使得网络变得非常不稳定，在极端的情况下，权重值变得非常大，以至于溢出，导致NaN值。在深层感知机网络中，梯度爆炸会导致网络不稳定，最好的结果是无法从训练数据中学习，最坏的结果是出现无法再更新的NaN权重值。在RNN中，梯度爆炸最好的结果是网络无法学习长的输入序列数据。

怎样判定出现了梯度爆炸的现象？

221125

字典的get方法：

dict.get(key,default)：查看键是否存在，若存在返回键值，若不存在，则返回指定的default值。

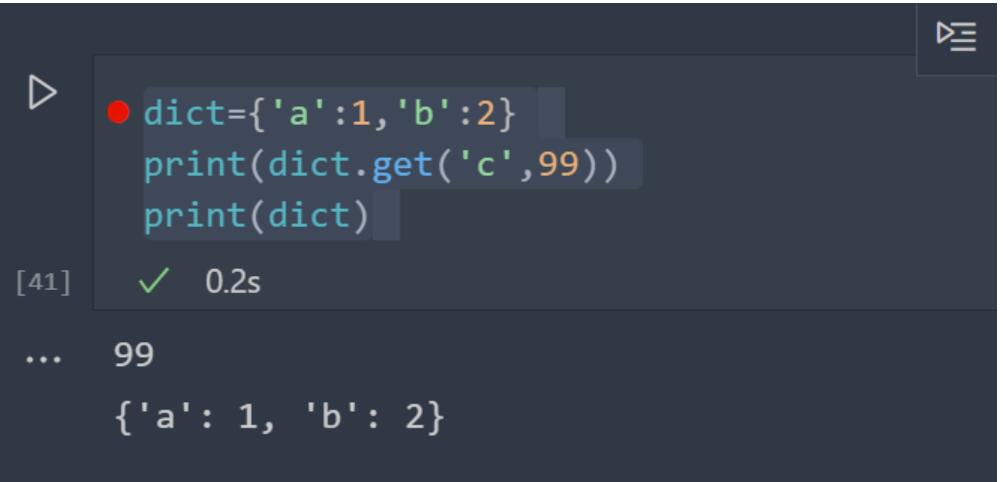
注意：若不存在该键，也不会创建该键并赋值。

np.logspace()方法：

用于构造log等比数列，

np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0):

start：代表序列的起始值。

stop：代表序列的终止值。

num：生成的序列数个数。

endpoint：布尔类型值，默认是true。如果为true, ‘stop’是最后一个样本；否则，它不包括在内。

base：代表序列空间的底数，默认基底为10。

dtype：代表序列数组项的数据类型。

eg：从10^-4到10^0按照等比数列生成20个数。

np.random.rand():

生成[0,1)之间服从高斯分布的size个数

np.pad()：

补零。https://blog.csdn.net/baicaiBC3/article/details/123380479

221126

PyTorch学习：

如何构造层和块：

1
2
3
4
5
6
7
8
9
import torch
from torch import nn
from torch.nn import functional as F

#单层神经网络：线性层-relu-线性层
net=nn.Sequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10))
X=torch.rand(2,20) #2*20的随机矩阵，2是批量大小，20是输入的数据的维度（特征数）
net(X)
#输出2*10

module：任何一个层和一个神经网络都可以认为是module的一个子类。

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#自定义一个MLP类实现相同的功能
class MLP(nn.Module): 
	def __init__(self):
		super()._init__() #继承父类
        #定义两个全连接层，存在类的成员变量中
		self.hidden = nn.Linear(20,256)
        self.out = nn.Linear(256,10)
    #前向传播的实现 forward函数,输入参数X
    #输入X放到hidden层中，得到隐层的输出，然后到relu层激活，再做一次out
    #实现了线性层-relu-线性层
	def forward(self,X):
		return self.out (F.relu(self.hidden (x)))
#定义一个MLP，是nn.Module的子类，继承nn.Module的所有函数

#如何调用？
net=MLP() #将类实例化
net(X) #调用
  
1
2
3
4
5
6
7
8
9
10
11
class MySequential(nn.Module):
    def __init__(self, *args):  #*args: list of arguments
        super.__init__()
        for block in args:
            self._modules[block]=block #层 ordered dict
    def forward(self,X):
        for block in self._modules.values():
            X=block(X)
        return X
net=MySequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10)) 
net(X)

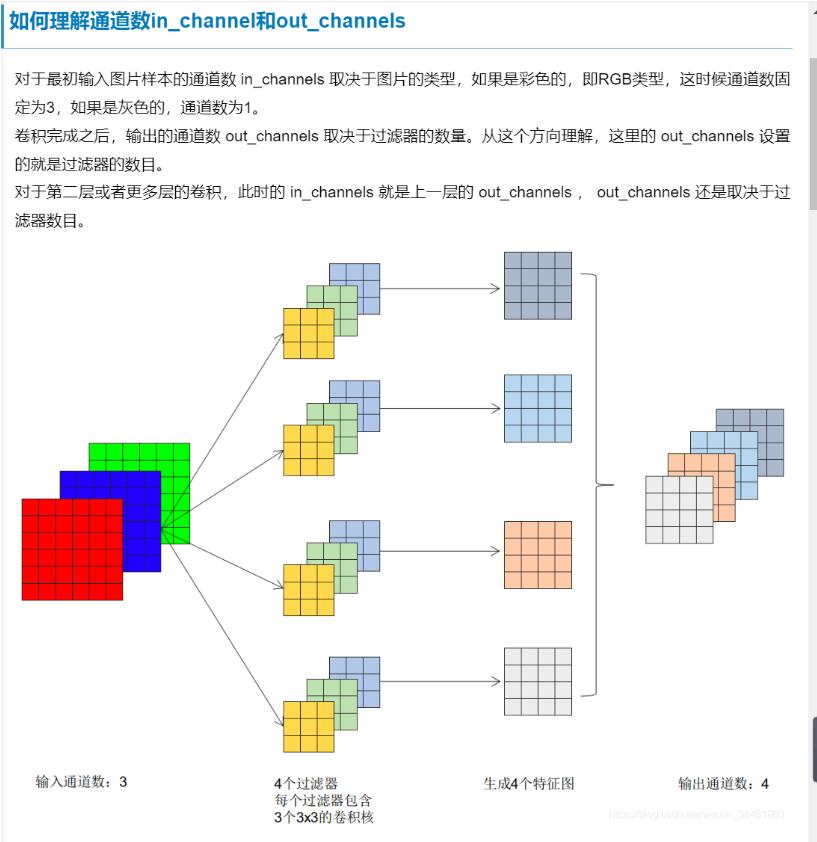
如何理解通道数in_channels和out_channels:

img